堆的定义
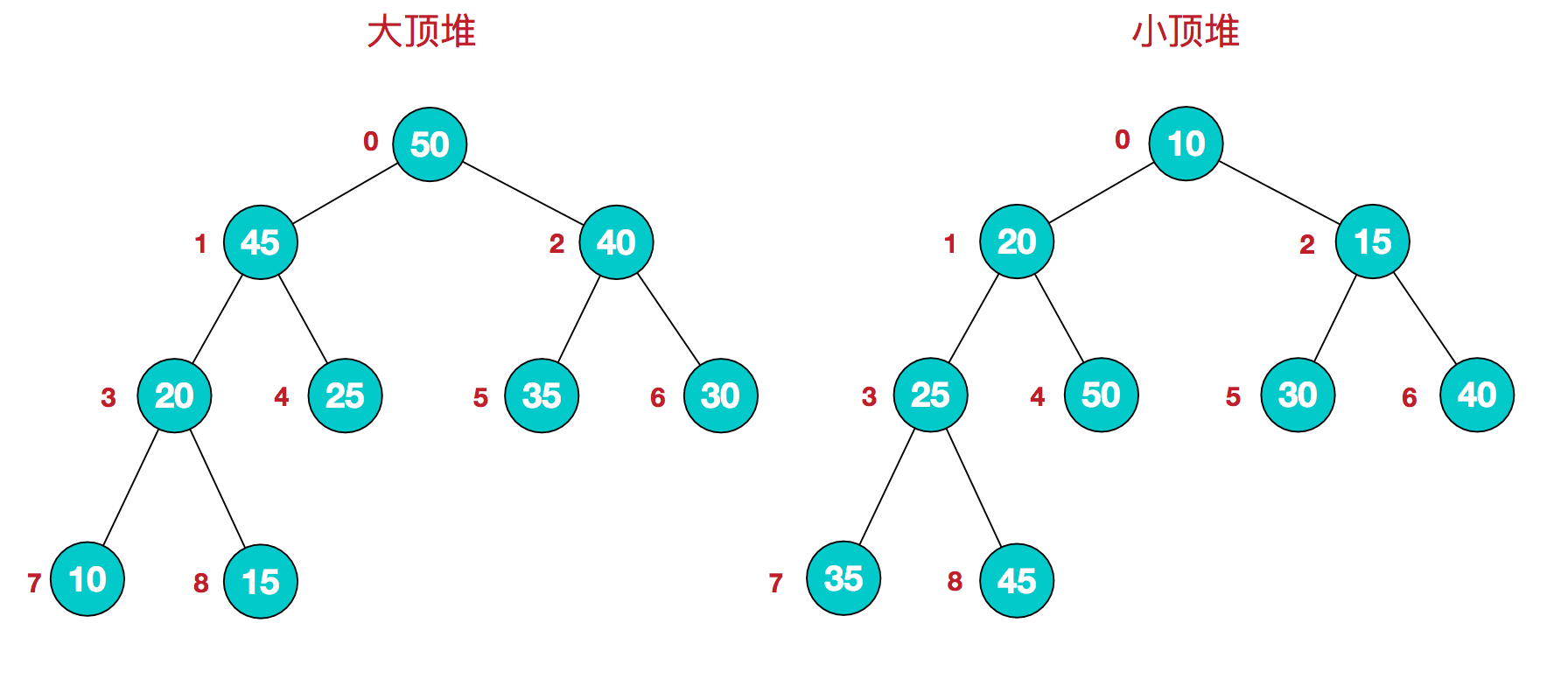
堆一种特殊的完全二叉树。它的特殊之处体现在每个节点与子节点的比较上。父节点比子节点大的叫大顶堆。父节点比子节点小的叫小顶堆。如下图所示。
这里需要注意一下堆和二叉搜索树的区别。
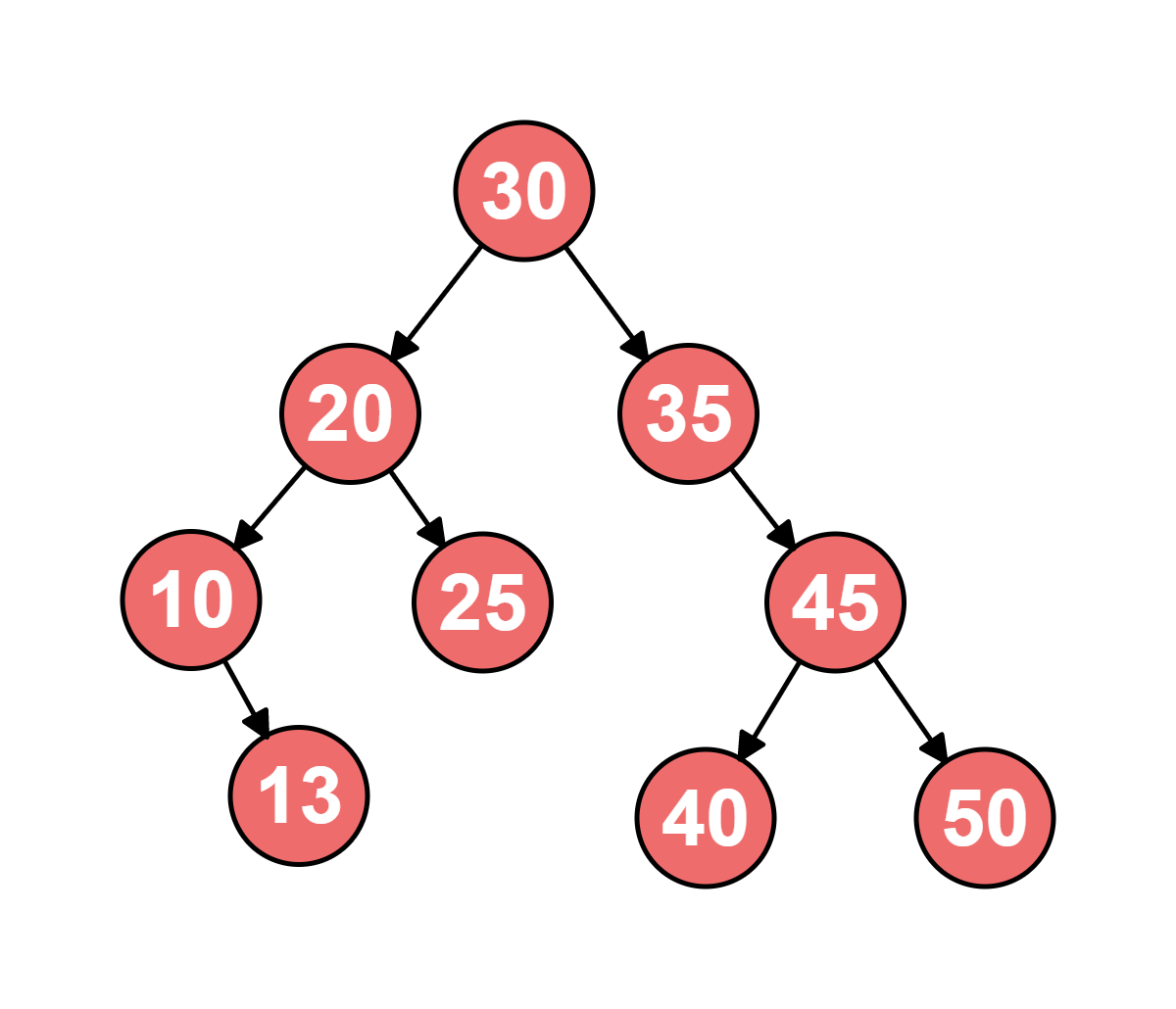
可以看到,首先二叉搜索树并不要求是完全二叉树,其次根节点也不一定是最值。但是要求左子树<该节点<右子树(或者>),递归成立。而堆并不要求左右子树有序,只要保证父节点相对于左右孩子是最大或最小就可以。对二叉搜索树的中序遍历即有序数组。另外二叉搜索树之所以叫“搜索”,其作用也主要是用来查找(时间复杂度O(logn)),而堆是用来排序的,堆查找的时间复杂度为O(n)。
堆排序
下面以由小到大排序为例演示堆排序过程。
需要注意的是,升序排序要用大顶堆,降序排序用小顶堆。为什么?看完排序流程就明白了。
1.1 构造初始堆。
假设给定的无序数列为4,6,8,5,9。将其存储到数组arr中,对应位置和创建的初始堆如下。
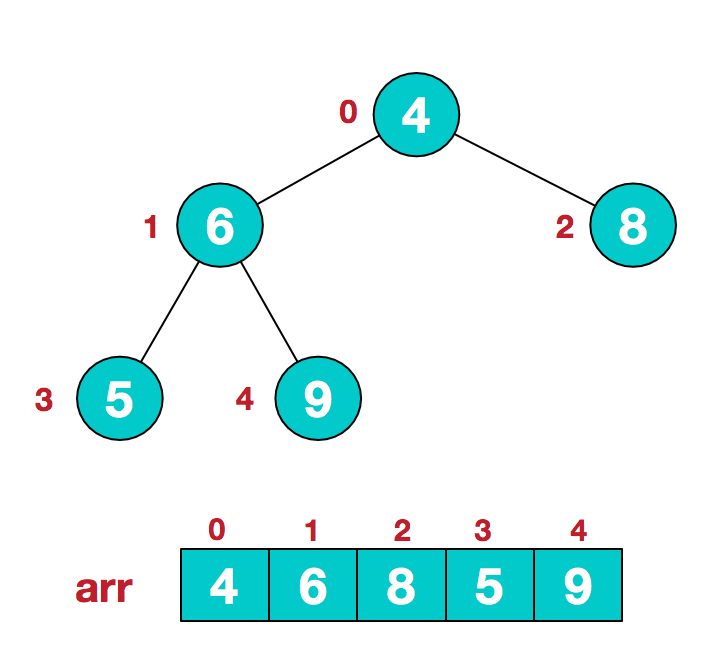
1.2 调整第一个非叶子节点
第一个非叶子节点为n/2-1,n为排序个数5,所以第一个节点下标为1,即数字6。
我们要调整成大顶堆,5<6<9,所以交换6和9。
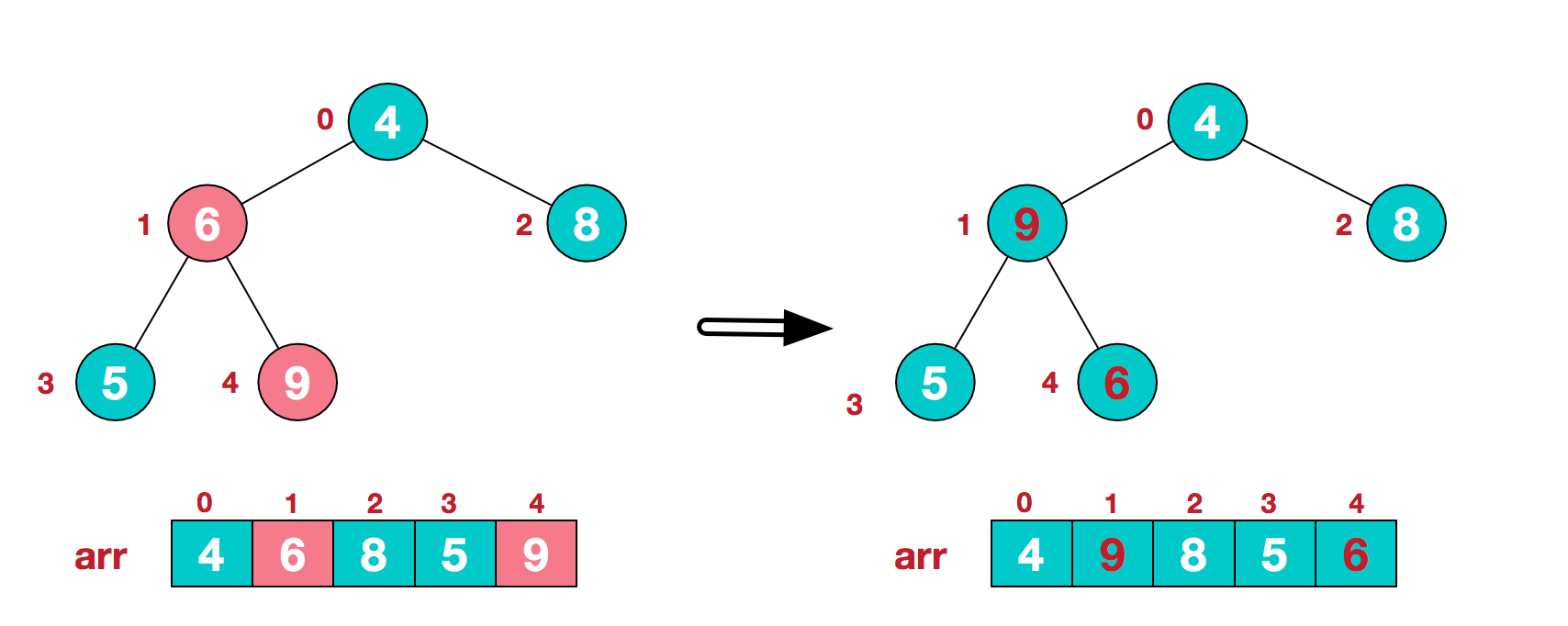
1.3 调整第二个非叶子节点
第二个非叶子节点为4,4<8<9,所以交换4,9。
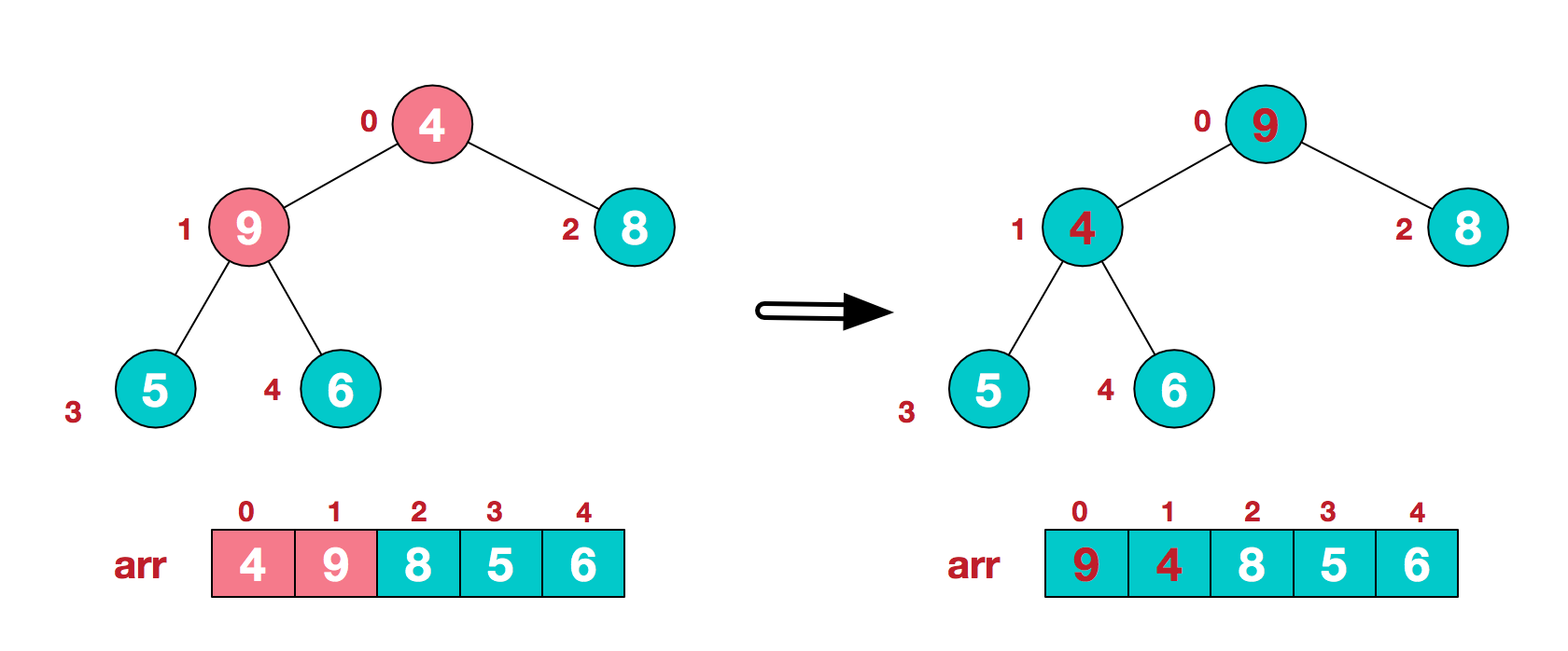
1.4 调整因根节点变化导致的子树结构
观察节点4,4<5<6,交换4,6。此时第一轮排序结束。
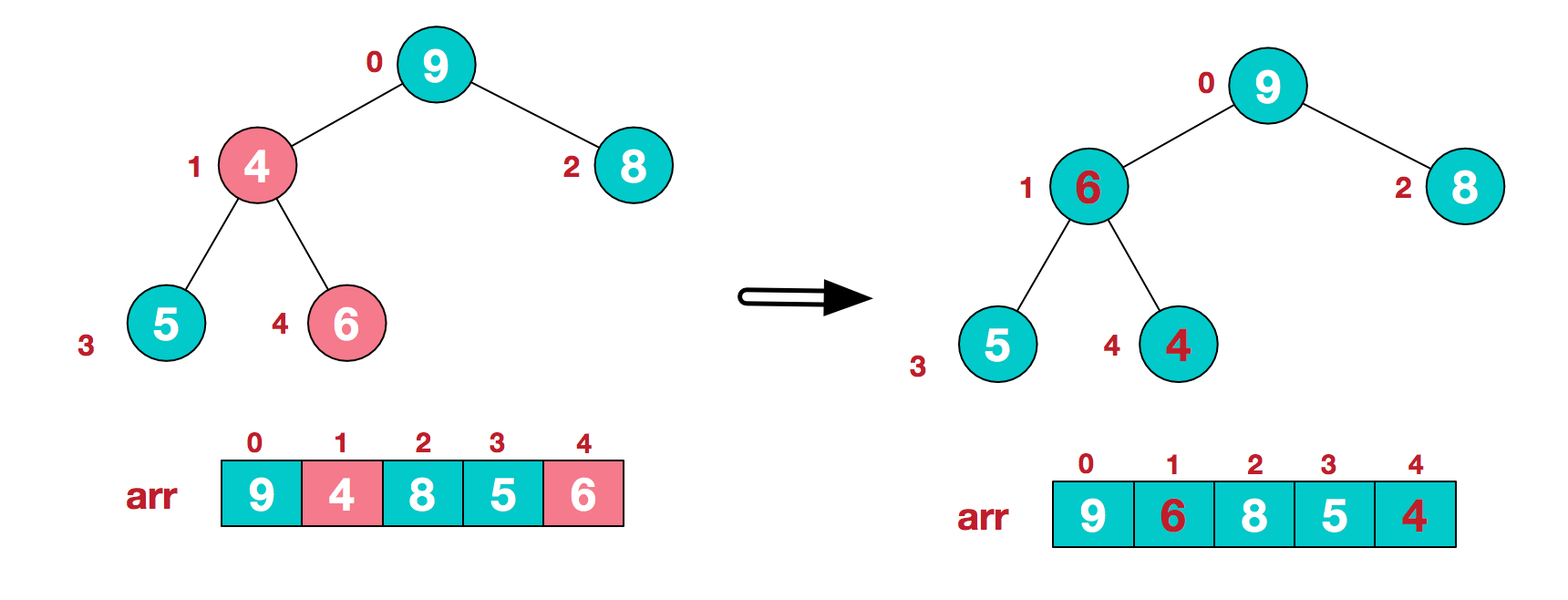
2.1 将堆顶与末尾交换,得到第一大元素
将堆顶元素与末尾元素进行交换,使末尾元素最大。以便后面调整对剩余数据排序。
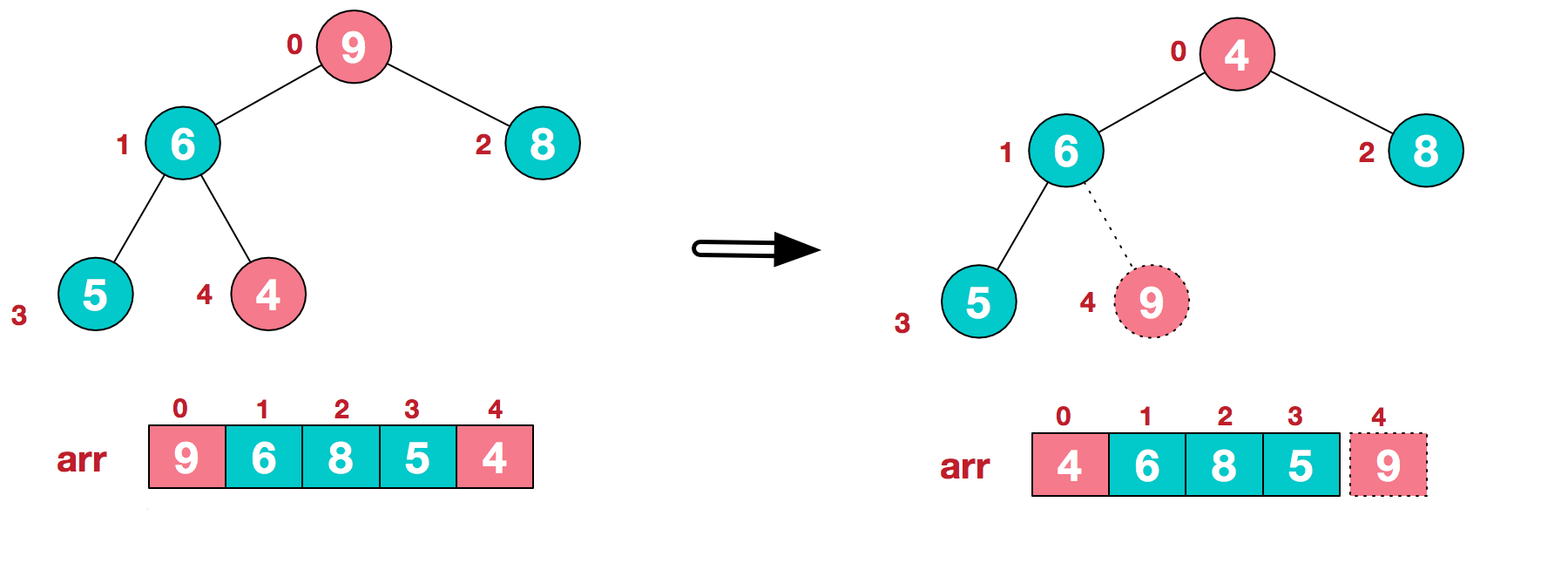
2.2 调整剩下的节点,使其满足大顶堆定义
6>5,不要调整,4<6<8,交换4,8
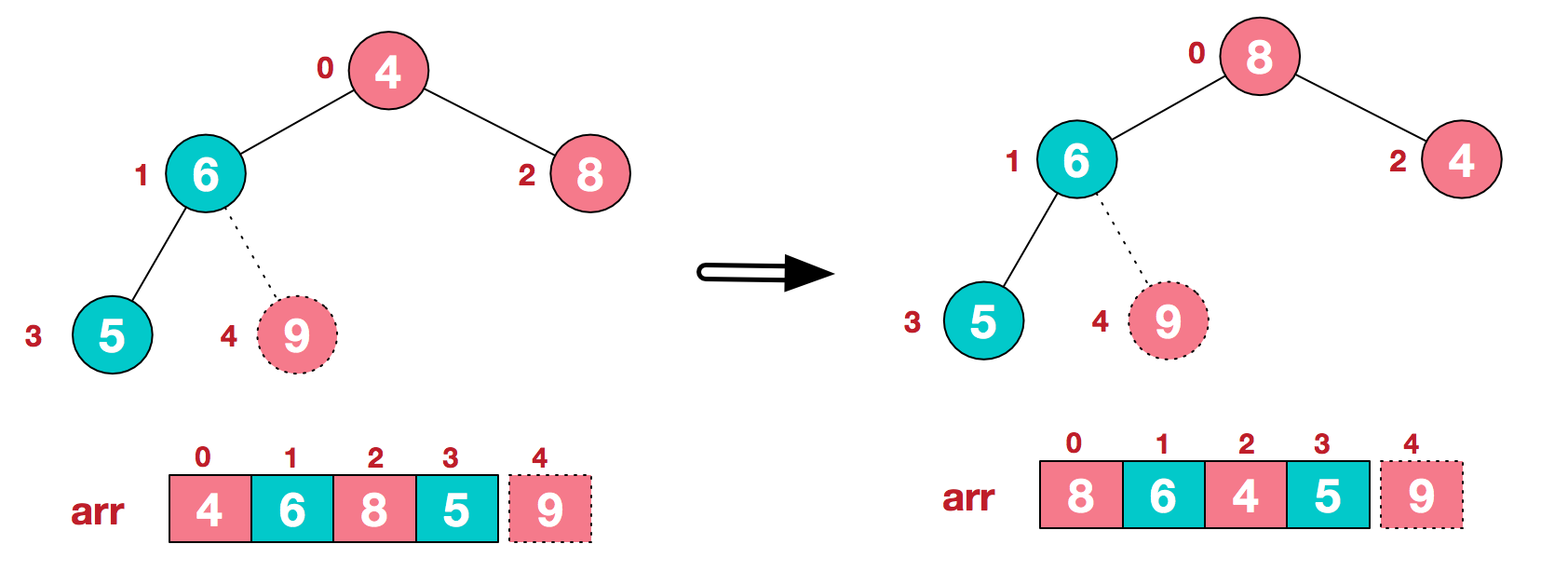
3.1 将堆顶元素8与末尾元素5进行交换,得到第二大元素8
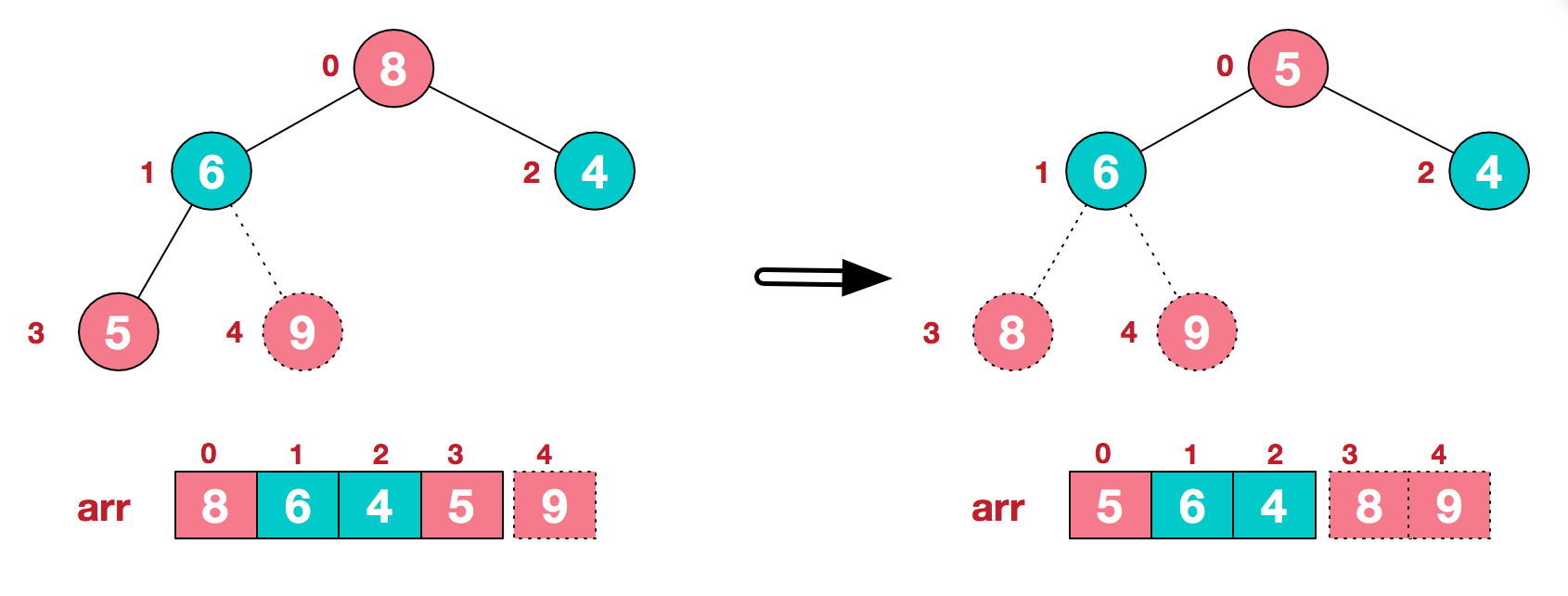
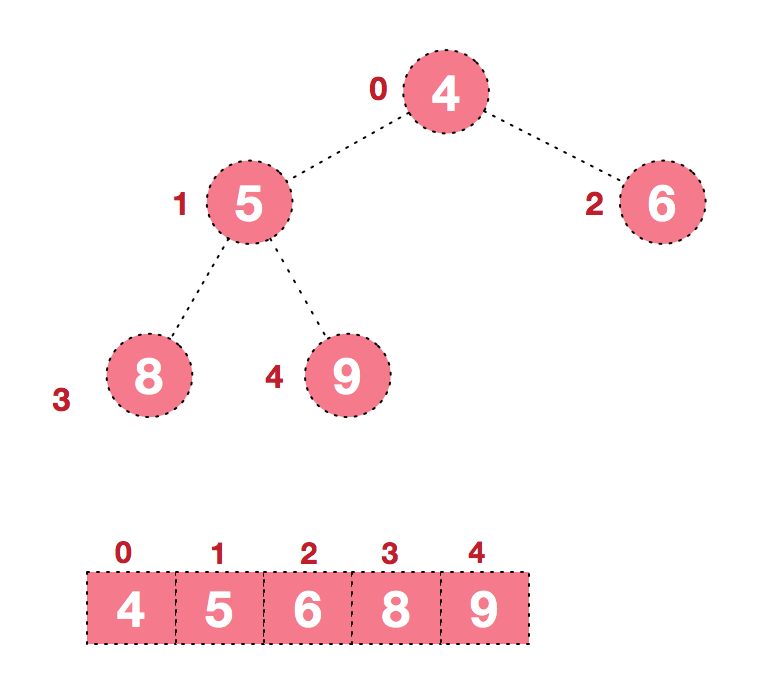
4.1 后续过程,继续进行调整,交换,如此反复进行,最终使得整个序列有序
优先队列(C++)
优先队列的实现就是堆。优先队列满足所有队列属性,只是在队列的基础上通过堆进行了排序,是有序的队列。默认队首是大元素,即降序排序,也即小顶堆的实现方法。
头文件
#include <queue>定义
格式:priority_queue<Type, Container, Functional>
- Type 数据类型
- Container 容器类型(Container必须是用数组实现的容器,比如vector,deque等等,但不能用 list。STL里面默认用的是vector)
- Functional 就是比较的方式
当需要用自定义的数据类型时才需要传入这三个参数,使用基本数据类型时,只需要传入数据类型,默认是大顶堆
// 默认降序,小顶堆
priority_queue<int> downPQ;
// 也可以定义成如下格式
priority_queue<int,vector<int>,less<int>> downPQ1;
// 升序排序,大顶堆
priority_queue<int,vector<int>,greater<int>> upPQ;操作方法
- top 访问队头元素
- empty 队列是否为空
- size 返回队列内元素个数
- push 插入元素到队尾 (并排序)
- emplace 原地构造一个元素并插入队列
- pop 弹出队头元素
- swap 交换内容
例子
降序排序
// CPP Program to demonstrate Priority Queue
#include <iostream>
#include <queue>
using namespace std;
void showpq(const priority_queue<int> &gq)
{
priority_queue<int> g = gq;
while (!g.empty()) {
cout << '\t' << g.top();
g.pop();
}
cout << '\n';
}
// Driver Code
int main()
{
priority_queue<int> gquiz;
gquiz.push(10);
gquiz.push(30);
gquiz.push(20);
gquiz.push(5);
gquiz.push(1);
cout << "The priority queue gquiz is : ";
showpq(gquiz);
return 0;
}Output:
The priority queue gquiz is : 30 20 10 5 1【参考】