1. 简介

FLAME是一个关于人脸的参数化模型。所谓参数化模型，通俗来说是指通过调整参数（如形状参数、姿态参数、表情参数等）可以控制生成的最终模型长什么样。类似的还有人体参数化模型SMPL，SMPL-X等。

通过训练多个数据集不同人脸（早期人脸模型是通过扫描中性表情的年轻欧洲人建立的），将身份(indentity)、姿态(pose)和面部表情(facial expression)特征分离开来。FLAME包含了一个形状(shape)空间变量、连接头部的脖子、可旋转的眼球组成。可以通过学习表情混合形状(expression blendshapes)捕捉面部非刚性形变。

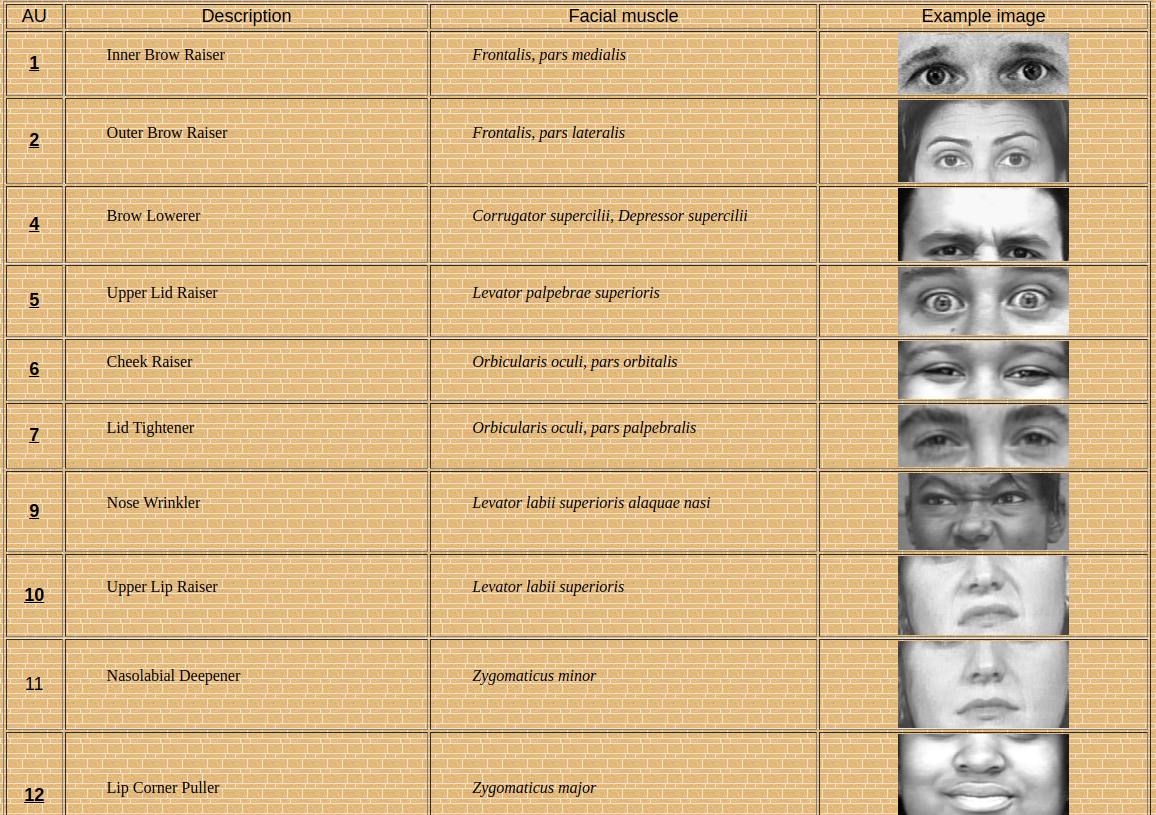
还有一种求解面部表情blenshapes的方法，是基于面部表情单元(FACS)实现的。FACS多个设置可能会产生相同的表情结果，这使得从数据中求解参数变得复杂。FLAME采用标准正交表达式，充分考虑了identity和pose。这对于稀疏数据和噪声的拟合效果更好。

FACS

2. 训练数据集

CAESAR：使用了大约4000个身体扫描的头部，包含了不同年龄、性别
D3DFACS：400个4D人脸捕捉序列，为姿态(pose)和表情(expression)建模

3. 模型公式

延用了SMPL的方法建模。不同的是，SMPL没有模拟面部姿势和表情，且身体的姿态是由于刚体形变产生的，而面部表情许多形变都是由于肌肉产生的非刚体形变。

FLAME使用标准的基于顶点的线性混合蒙皮(linear blend skinning, LBS)与校正的混合形状(blendshapes)。

顶点N=5023
关节点K=4, 包括脖子，下吧，两个眼球

表达形式： $M(\vec{\beta},\vec{\theta},\vec{\psi}):\Bbb R^{|\vec{\beta}|\times|\vec{\theta}|\times|\vec{\psi}|}\to\Bbb R^{3N}$

$\vec{\beta}$ ：形状shape参数
$\vec{\theta}$ ：姿态pose参数，$\vec{\theta}\in\Bbb R^{3K+3}$，包含$K+1$个轴角(aix-angle)坐标系的旋转向量
$\vec{\psi}$ ：表情expression参数
$N$ : 顶点

更具体地，公式可以定义如下：

$$
\begin{equation}\begin{split}
M(\vec{\beta},\vec{\theta},\vec{\psi})&=W(T_P(\vec{\beta},\vec{\theta},\vec{\psi}),\mathbf{J}(\vec{\beta}),\theta,\mathbf{\mathcal{W}})
\end{split}\end{equation}
$$

$W(\overline{\mathbf{T}},\mathbf{J},\vec{\theta},\mathbf{\mathcal{W}})$ 标准蒙皮函数。用于旋转关节$\mathbf{J}\in \Bbb{R}^{3K}$附近的顶点$\overline{\mathbf{T}}$，并由混合权重(blendweights) $\mathbf{\mathcal{W}}\in \Bbb{R}^{K\times N}$进行线性平滑。

其中$T_P(\vec{\beta},\vec{\theta},\vec{\psi})$表示了形状、姿态、表情相对于网格模板的偏移量。

$$
\begin{equation}\begin{split}
T_P(\vec{\beta},\vec{\theta},\vec{\psi})=\overline{\mathbf{T}} + B_S(\vec{\beta}, \mathbf{\mathcal{S}})+B_P(\vec{\theta}, \mathbf{\mathcal{P}})+B_E(\vec{\psi},\varepsilon)
\end{split}\end{equation}
$$

$\overline{\mathbf{T}} \in \mathbb{R}^{3N}$ 网格模板/平均网格脸
$B_S(\vec{\beta}; \mathbf{\mathcal{S}}): \Bbb{R}^{|\vec{\beta}|} \to \Bbb{R}^{3N}$ 形状blendshape函数。解释与identity相关的形状变化
$B_P(\vec{\theta}; \mathbf{\mathcal{P}}): \Bbb{R}^{|\vec{\theta}|} \to \Bbb{R}^{3N}$ 姿态blendshape函数。解决线性混合蒙皮不能解决的姿态形变问题。
$B_E(\vec{\psi};\varepsilon): \Bbb{R}^{|\vec{\psi}|} \to \Bbb{R}^{3N}$ 表情blendshape函数，用来捕捉面部表情。

由于不同的脸部形状会产生不同的关节位置，所以关节定义成面部形状的函数

$$
\begin{equation}\begin{split}
\mathbf{J}(\vec{\beta};\mathcal{J},\mathbf{\overline{T}},\mathbf{\mathcal{S}}) = \mathcal{J}(\mathbf{\overline{T}}+B_S(\vec{\beta}; \mathbf{\mathcal{S}}))
\end{split}\end{equation}
$$

$\mathcal{J}$ 稀疏矩阵，定义了如何从网格顶点计算关节位置

形状混合：通过线性混合形状建模得到不同对象的形状变化

$$
\begin{equation}\begin{split}
B_S(\vec{\beta}; \mathbf{\mathcal{S}}) = \sum_{n=1}^{|\vec{\beta}|} \beta_n \mathbf{S}_n
\end{split}\end{equation}
$$

$\vec{\beta}=[\beta_1,\ldots,\beta_{|\vec{\beta}|}]^T$ 形状shape系数
$\mathbf{\mathcal{S}}=[\mathbf{S}1,\ldots,\mathbf{S}{|\vec{\beta}|}]\in\mathbb{R}^{3N\times|\vec{\beta}|}$ 形状正交基，由PCA方法得到

姿态混合

$$
\begin{equation}\begin{split}
B_P(\vec{\theta}; \mathbf{\mathcal{P}}) = \sum_{n=1}^{9K} (R_n(\vec{\theta})-R_n(\vec{\theta}^\ast)) \mathbf{P}_n
\end{split}\end{equation}
$$

$\vec{\theta}^\ast$ zero pose
$R(\vec{\theta}):\mathbb{R}^{|\vec{\theta}|}\to\mathbb{R}^{9K}$ 是一个从脸部/头部/眼睛姿势向量$\vec{\theta}$到连接关节旋转矩阵的函数
$\mathbf{P}_n\in\mathbb{R}^{3N}$ 描述了从$R_n$得到的与静态位姿的顶点偏移。
$\mathcal{P}=[\mathbf{P}1,\ldots,\mathbf{P}{9K}]\in\mathbb{R}^{3N\times9K}$ 姿态空间，包含了所有姿态混合

表情混合：由线性blendshapes修改得到

$$
\begin{equation}\begin{split}
B_E(\vec{\psi}; \varepsilon) = \sum_{n=1}^{|\vec{\psi}|} \vec\psi_n \mathbf{E}_n
\end{split}\end{equation}
$$

$\vec{\psi}=[\psi_1,\ldots,\psi_{|\vec{\psi}|}]^T$ 表情expression系数
$\varepsilon=[\mathbf{E}1,\ldots,\mathbf{E}{|\vec{\psi}|}]\in\mathbb{R}^{3N\times|\vec{\psi}|}$ 表情正交基，训练得到

形状模板Template shape

注意，形状，姿势和表情blendshape都是模板网格$\mathbf{\overline{T}}$的位移。我们从一个通用的脸模板网格开始，然后从扫描和模型的其余部分学习$\mathbf{\overline{T}}$。

马捷径

https://molianwh.github.io/2022/06/26/cv/flame-lun-wen-jie-du/