一、基础知识
1. 卷积与全连接的区别
卷积相比全连接两大特性:区域连接、权值共享
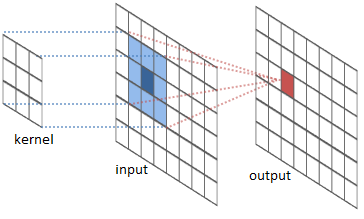
- 区域连接:由于卷积核远小于输入尺寸,输出层上的节点只与输入层上部分节点关联。
- 权值共享:由于卷积核的滑动机制,输出层不同位置节点与输入层连接权值相同,即使用的卷积核参数相同。
- 结构不变:针对二维输入,输出也是二维。但是全连接输入图片,输出将变成扁平的一维数组。
2. 计算
- 输出大小
$$output=(input+2 \times padding-kernel)/stride +1 \tag{1}$$
如果除法遇到非整除情况,采用向下取整。计算时,放弃输入左上侧数据,使卷积核刚好能滑动到右下角。
- 感受野大小
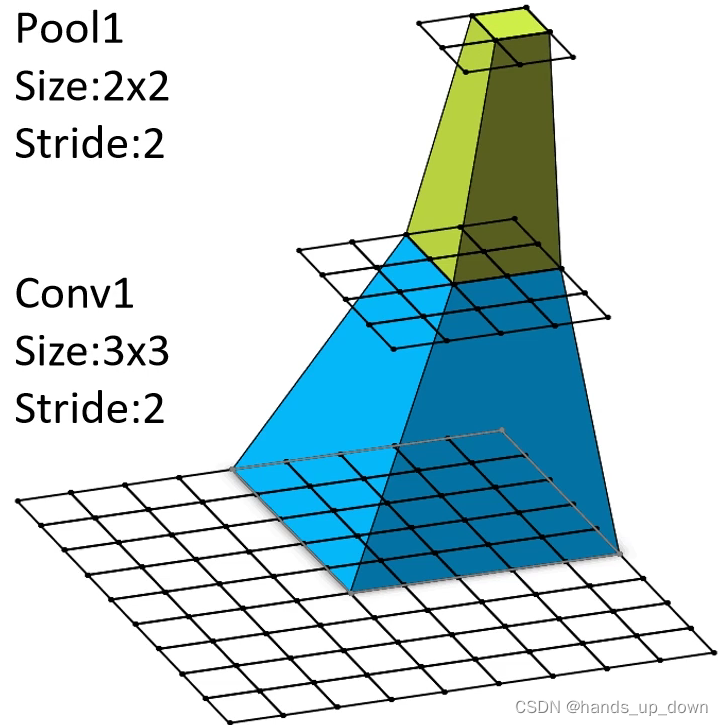
感受野定义:在某层输出(特征图)上一个像素点对应的原图的区域大小。
第0层感受野 $R_0=1$
对照图可以看到,计算i层的感受野$R_i$就相当于$(1)$式中的$input+2padding$,$R_{i-1}$相当于$kernel_{i-1}$,$kernel_{i}$相当于$output$。所以有
$$(kernel_i-1) \prod_{j=0}^i stride_j +R_{i-1} = R_i \tag{2}$$
- 参数个数
在通道概念上,输入到输出本质是全连接。对于输入通道数$cannel_{input}$,输出通道数$cannel_{output}$,一共对应了$cannel_{output}$个卷积核,每个卷积核通道数$cannel_{input}$。总参数量:
$$cannel_{input} \times cannel_{output} \times kernel_{width} \times kernel_{height} \tag{3}$$
3. padding方式
$padding=same$
左右一共添加$kernel-1$列,上下同理。即
$$2 \times padding = kernel-1 $$
$padding=valid$
即不填充,$padding =0$
二、卷积变种
- 分组卷积
- 转置卷积(反卷积)
- 空洞卷积
- 可形变卷积
1. 分组卷积
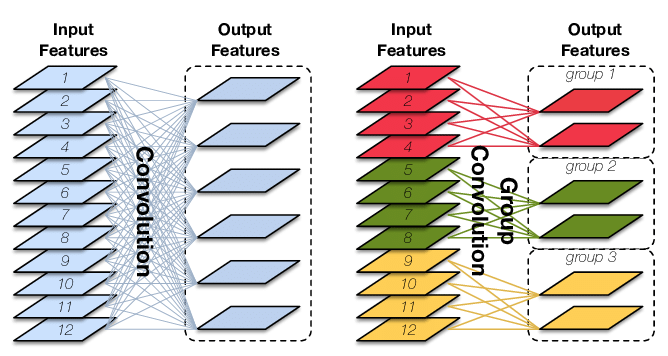
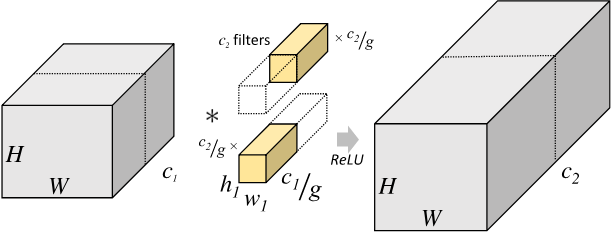
前面说过,普通卷积在通道概念上是全连接的,如分组卷积(1)的左图所示。输入的通道数对应卷积核通道数,输出通道数对应卷积核个数。
分组卷积对所有输入输出和卷积核做相同分组。只在对应组内是全连接。
最初分组卷积用于解决多GPU训练。现在更多用于移动端小型网络
2. 转置卷积
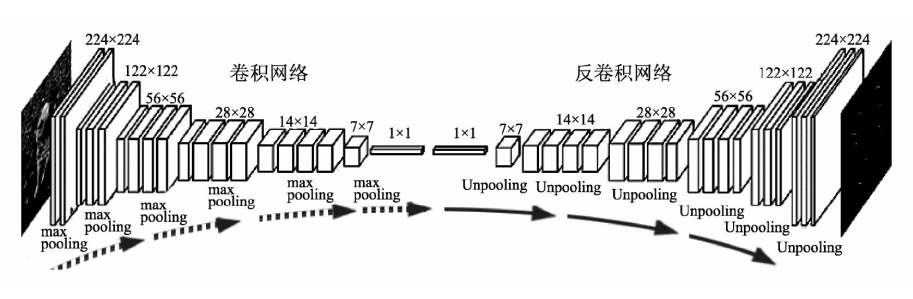
转置卷积又叫反卷积,其操作看图就明白了。它可以将输入到输出的尺寸逆转回来。
值得注意的是,逆转的操作只针对尺寸,不针对数值。
转置卷积本质是对输入数据做补零或上采样操作。
普通卷积与转置卷积的任务不同。普通卷积用来特征提取,压缩特征图尺寸;转置卷积用来上采样或扩张特征图。
转置卷积应用场景:
语义分割/实例分割
物体检测、关键点检测:需要输出与原图大小一致热图
图像自编码器、变分自编码器、生成式对抗网络
3. 空洞卷积
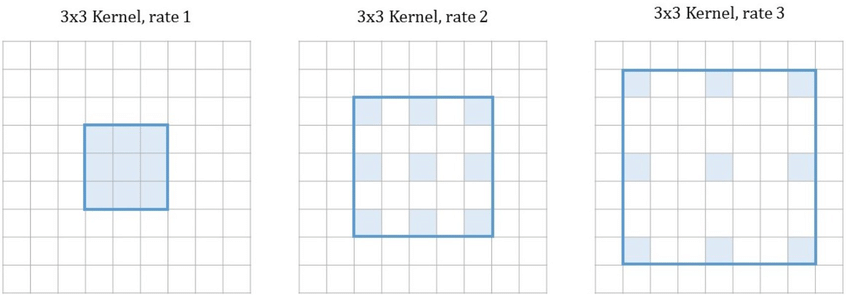
空洞卷积是在每个值之间插入“空洞”。
扩张率为$r$的空洞卷积,在相邻点之间有$r-1$个空洞。扩张率是个超参数。
空洞卷积作用:
- 扩大卷积核尺寸
- 扩大感受野(非下采样)
- 保留输入数据内部结构
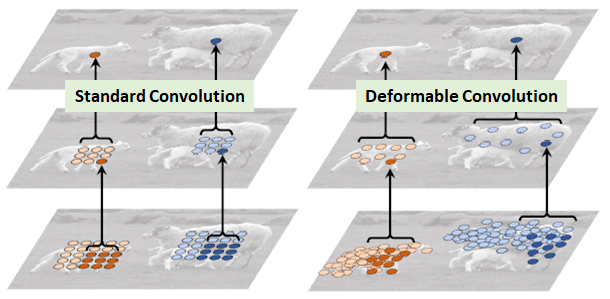
4.可形变卷积
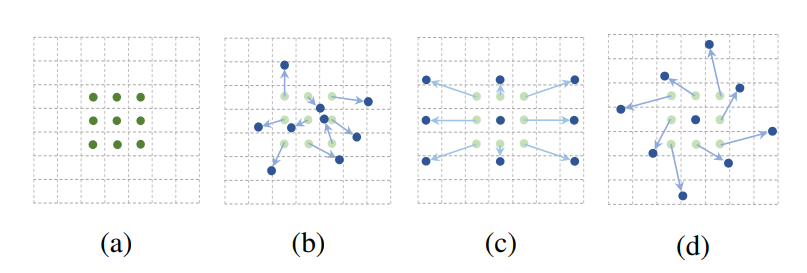
可形变卷积平行地学习了卷积值采样点的偏移量。使之可以自适应目标的尺寸、形态。
三、卷积神经网络基础模块
1. 批归一化
批归一化的作用:
确保网络各层即使参数发生变化,输入输出的分布保持稳定,避免内部协变量偏移。采用批归一化处理,训练更稳定,对初始值不再敏感,可以使用较大的学习率快速达到收敛。
在实践过程中,业界倾向于将批归一化置于激活函数后。
2. 卷积层
可以将卷积层理解为为多层感知机提取非线性特征。
由于卷积核是局部连接,提取的局部特征,对位置不敏感,因此解决不同位置有哪些元素这样的高层语义信息比较好。但是无法提取不同位置元素之间的联系。
3. 全连接层
与卷积层不同,全连接层的每个输出与所有输入都有连接,所以对位置敏感。可以提取不同位置间的联系。比如眼睛和嘴的位置正确才能构成人脸。
在分类问题中,全连接层一般放在卷积层后,即卷积神经网络的最后几层通常是全连接层。有时也用全局平均池化替代,优点是参数少。
4. 瓶颈结构
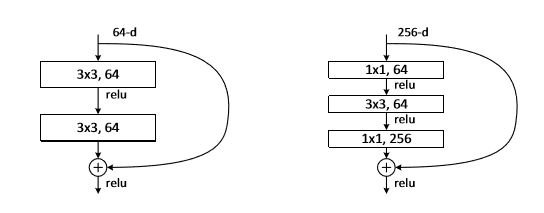
由一个$1\times1$的卷积压缩大卷积层输入特征图通道数,处理结束后再用一个$1\times1$恢复通道。
瓶颈结构可以大大减少参数量,降低计算量。同时增加了网络层数,增大感受野,提升特征提取能力。
瓶颈结构可以用于所有的卷积神经网络中。如目标检测、分割、生成式对抗网络。
5. 沙漏结构
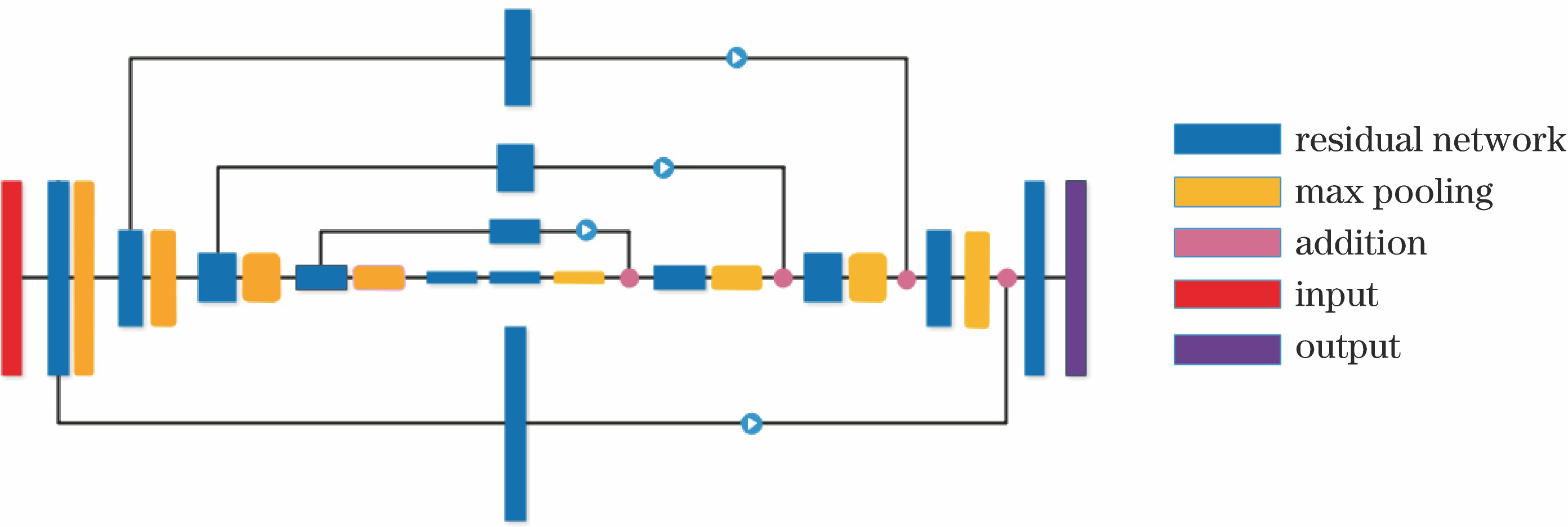
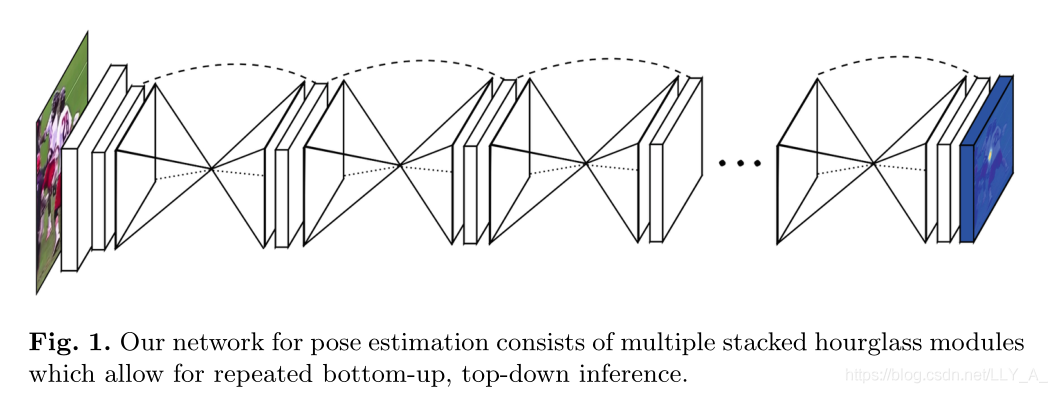
沙漏结构类似于瓶颈结构,比瓶颈结构尺寸更大,涉及层数更多。包括两个分支:
- 编码器:(自底向上),利用卷积、池化等操作压缩特征。
- 解码器:(自顶向下),利用反卷积、插值上采样,扩大尺寸(通道可能减少)。
沙漏结构具有以下作用:
- 多尺度特征融合
- 提升感受野,增强对小尺寸但又依赖上下文的物体感知能力,如人体关节点。
四、常见的卷积神经网络
这里不详细介绍每种网络。
AlexNet
- 简单的堆叠卷积层、池化层
VGGNet
- 使用更小的卷积核,3×3或5×5
Inception
- 使用瓶颈结构
ResNet
- 使用跳层连接shortcut